रचनीय संख्याओं का विलक्षण संसार

प्राचीन ग्रीसवासी ज्यामितीय रचनाओं में विशेष रुचि रखते थे. वे विशेषकर वैसी रचनाओं में रुचि रखते थे, जिनकी रचनाएँ केवल पैमाने (जिसपर केवल इकाई दूरी अंशांकित हों) और परकार की सहयता से किया जा सके. उन्हें समबाहु त्रिभुज, वर्ग, समपंचभुज, समषट्भुज इत्यादि की रचनाओं का ज्ञान था. उन्हें किसी कोण को समद्विभाजित करने का भी ज्ञान था. परन्तु, समसप्त्भुज की रचना कैसे की जाए या किसी कोण को कैसे समत्रिभाजित किया जाए - इनके बारे में उन्हें कोई जानकारी नहीं थी. इसके अतिरिक्त ज्यामितीय रचनाओं से संबंधित कुछ और भी समस्याएँ थीं, जो उनके लिए असाध्य थीं. जैसे कि किसी वृत्त के क्षेत्रफल के बराबर वर्ग की रचना या किसी घन के आयतन के दुगुने आयतन वाले घन की रचना, इत्यादि. इन समस्याओं ने गणितज्ञों को 2000 वर्षों तक उलझाए रखा. इन समस्याओं का समाधान 19वीं शताब्दी में संभव हो सका, जब इन ज्यामितीय समस्याओं को बीजगणितीय समस्याओं के रूप में परिवर्तित किया गया. वास्तव में उपरोक्त समस्याओं की रचनाएँ संभव नहीं है. अतः इन रचनाओं में मिली असफलता स्वाभाविक थी. बीजगणित के माध्यम से इन समस्याओं के अध्ययन के क्रम में दो नई प्रकार की संख्याओं का उद्गम हुआ - रचनीय संख्याएँ और अरचनीय संख्याएँ. प्रस्तुत लेख में हम इन विषयों पर विस्तार से चर्चा करेंगे.

चित्र - 1: वास्तविक संख्याओं का वर्गीकरण

वास्तविक संख्याओं को उनके लक्षणों के आधार पर कई वर्गों में वर्गीकृत किया जा सकता है. उदाहरण के लिए, प्राकृत संख्याओं को विभाज्यता के आधार पर सम (even) और विषम (odd) संख्याओं में, गुणनखंड के आधार पर अभाज्य (prime) और भाज्य (composite) संख्याओं में, परिमेयता के आधार पर परिमेय (rational) और अपरिमेय (irrational) संख्याओं में वर्गीकृत किया जा सकता है.  आइए, हम वास्तविक संख्याओं के एक अन्य लक्षण पर विचार करते हैं. यह लक्षण है - रचनीयता. इस लक्षण के आधार पर हम वास्तविक संख्याओं को दो प्रकार की संख्याओं में वर्गीकृत करते हैं - रचनीय संख्याएँ (constructible numbers) और अरचनीय संख्याएँ  (non-constructible numbers). जैसा कि नाम से ही स्पष्ट है - रचनीय संख्या का अर्थ है - वैसी संख्या जिसकी रचना की जा सके. रचना से हमारा तात्पर्य है - वास्तविक संख्या रेखा (real number line) पर किसी संख्या का ज्यामितीय निरूपण. इन संख्याओं की रचना हेतु हम केवल दो ज्यामितीय उपकरणों - पैमाना (ruler) और परकार (compass) का प्रयोग करेंगे. इस पैमाने पर केवल इकाई दूरी (unit length) और इसके पूर्णांकीय दूरी अंशांकित होंगे (चित्र - 2 देखें). सैद्धांतिक रूप से हम इस पैमाने को अनंत लम्बाई वाला मान सकते हैं. इस प्रकार रचनीय संख्याओं को हम निम्न प्रकार परिभाषित कर सकते हैं:

रचनीय संख्याएँ वैसी वास्तविक संख्याएँ हैं, जिनका ज्यामितीय निरूपण संख्या रेखा पर केवल उपरोक्त वर्णित पैमाना और परकार की सहायता से किया जा सके. वैसी संख्याएँ जो रचनीय संख्याएँ नहीं हैं, अरचनीय संख्याएँ कहलाती हैं.

चित्र - 2: पैमाना और परकार

क्या अब आप कुछ रचनीय संख्याओं का उदाहरण दे सकते हैं ? पूर्णांको के विषय में आपका क्या विचार है ? संख्या रेखा पर पूर्णांकों के निरूपण से हम सभी परिचित हैं. इनका निरूपण केवल पैमाना और परकार की सहायता से किया जा सकता है. अतः ये संख्याएँ रचनीय संख्याएँ हैं. पैमाना की सहायता से एक संख्या रेखा खींचिए. इस पर पैमाने की सहायता से $0$ और इससे इकाई दूरी पर $1$ अंकित कीजिये. अब परकार की सहायता से हम किसी भी धनात्मक या ऋणात्मक पूर्णांक को इस संख्या रेखा पर निरूपित कर सकते हैं.

चित्र - 3: संख्या रेखा पर पूर्णांकों का निरूपण

पूर्णांक संख्याएँ रचनीय संख्याएँ हैं.

अब यदि दो पूर्णांक $a$ और $b$ दिए हुए हों, तो हम संख्या रेखा पर $a + b$ को आसानी से निरूपित कर सकते हैं (चित्र - 4 देखें). इसके लिए निम्नलिखित चरणशः प्रक्रिया अपनानी होती है:

1. एक पैमाना की सहायता से एक संख्या रेखा खींचिए और परकार की सहायता से इस पर पूर्णांक $a$ को अंकित कीजिए.
2. अब परकार की सहायता से पूर्णांक $a$ को केंद्र मानकर त्रिज्या $|b|$ का एक वृत्त खींचिए. यह वृत्त संख्या रेखा को दो बिंदुओं A और B पर प्रतिच्छेद करेगा. यदि $b$ धनात्मक हों, तो बिंदु $A$ संख्या $a + b$ को निरूपित करेगा. यदि $b$ ऋणात्मक हों, तो बिंदु $B$ संख्या $a + b$ को निरूपित करेगा.

चित्र - 4: संख्या रेखा पर $a + b$ का निरूपण

उदाहरण के लिए, नीचे के चित्र में $3 - 5$ और $- 3 + 5$ का निरूपण किया गया  है.

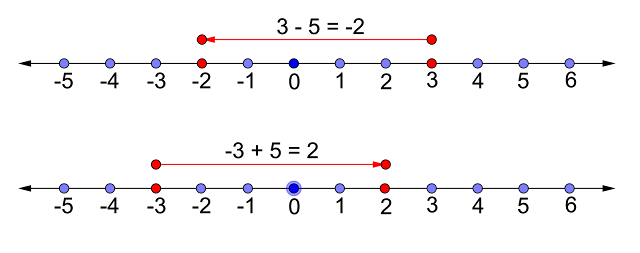चित्र - 5: संख्या रेखा पर $3 - 5 = -2$ और $- 3 + 5 = 2$ का निरूपण

अब मान लीजिये दो रचनीय संख्याएँ $a$ और $b$ दी हुई हैं, तो क्या $ab$ रचनीय संख्या होगी ? इस प्रश्न का उत्तर "हाँ " है. क्योंकि यदि $a$ एक धनात्मक रचनीय संख्या हों, तो इसके ऋणात्मक मान $-a$ को भी संख्या रेखा पर निरूपित किया जा सकता है, अतः किन्हीं दो धनात्मक रचनीय संख्याओं $a$ और $b$ के लिए ही $ab$ की रचनीयता दिखाना पर्याप्त है. इसे नीचे के चित्र में दिखाया गया है.

चित्र - 6: संख्या रेखा पर $ab$ का निरूपण

संख्या $ab$ की रचना के लिए चरणशः प्रक्रिया निम्नलिखित है:

1. पैमाने की सहायता से दो किरण AX और AY खींचिए जिससे कि $\angle XAY$ का मान $90$ डिग्री से कम हों.
2. किरण AX पर दो बिंदु B और C लीजिए जिससे कि $AB = 1$ और $AC = b$ हों. इसी प्रकार, किरण AY पर एक बिंदु D लीजिए जिससे कि $AD = a$ हों. 
3. अब बिंदु C से होते हुए BD के समांतर एक रेखाखंड CE खींचिए जो किरण AY को बिंदु E पर प्रतिच्छेद करता है. इसे बिंदु C पर $\angle CBD$ के बराबर $\angle XCE$ बनाकर किया जा सकता है.
4. अब बिंदु A को केंद्र मानकर त्रिज्या AE का एक चाप खींचिए जो किरण AX को बिंदु F पर प्रतिच्छेद करता है. तब $AF = ab$ होगा.

ध्यान दें कि $\triangle ABD$ और $\triangle ACE$ समरूप हैं. अतः समरूपता गुणधर्म केअनुसार,

\[\frac{AE}{AD} = \frac{AC}{AB} \Rightarrow \frac{AE}{a} = \frac{b}{1}\Rightarrow AE =ab.\] 

इसी प्रकार यदि दो रचनीय संख्याएँ $a$ और $b$ दी गई हों, तो हम $\frac{a}{b}$ को संख्या रेखा पर दर्शा सकते हैं (चित्र - 7) देखें. अतः परिमेय संख्या $\frac{a}{b}$ भी रचनीय संख्या होगी.

चित्र - 7: संख्या रेखा पर परिमेय संख्या $\frac{a}{b}$ का निरूपण

परिमेय संख्याएँ रचनीय संख्याएँ हैं.

अब तक हमने जाना.....

• परिमेय संख्याएँ रचनीय संख्याएँ हैं.
• पूर्णांक संख्याएँ रचनीय संख्याएँ है.
• यदि $a$ और $b$ दो रचनीय संख्याएँ हों, तो $a + b$, $a -b$, $ab$ और $\frac{a}{b}, b \neq 0$ रचनीय संख्याएँ होती हैं.
• इस प्रकार रचनीय संख्याएँ योग, व्यवकलन, गुणन और विभाजन की संक्रिया के सापेक्ष संवृत्त होती है.

 

अपरिमेय रचनीय संख्याएँ 

आइए हम कुछ अपरिमेय संख्याओं पर विचार करते हैं. उदाहरण के लिए, $\sqrt{2}$ पर विचार कीजिए. क्या इसे संख्या रेखा पर निरूपित किया जा सकता है ?

चित्र - 8: $\sqrt{2}$ का निरूपण

एक किरण AX लीजिए और इसपर एक बिंदु B लीजिए  जिससे कि $AB = 1$ हों. अब बिंदु B एक लम्ब रेखा BY की रचना कीजिए. इसपर एक बिंदु D लीजिए जिससे कि $BD = 1$ हों, रेखाखंड AD खींचिए. तब $\triangle ABD$ एक समकोण त्रिभुज है. अतः बौधायन प्रमेय के अनुसार,
\[AD = \sqrt{AB^2 + BD^2} = \sqrt{1+1} = \sqrt{2}.\]
अब बिंदु A को केंद्र मानकर त्रिज्या AD का एक चाप खींचिए जो किरण AX को बिंदु C पर प्रतिच्छेद करता है. तब स्पष्टतः $AC = \sqrt{2}$ है. इस प्रकार $\sqrt{2}$ एक रचनीय संख्या है. अत्यधिक व्यापक रूप में, किसी भी धनात्मक रचनीय संख्या $a$ के लिए $\sqrt{a}$ भी रचनीय संख्या होती है. इसे नीचे के चित्र में दिखाया गया है. एक रेखा खींचकर इस पर तीन बिंदु A, B और C इस प्रकार लीजिए कि $AB =1$ और $BC = a$ हों. अब AC को व्यास मानकर एक अर्धवृत्त ADC खींचिए. बिंदु B पर एक लम्ब रेखा BX खींचिए, जो इस अर्धवृत्त को बिंदु D पर प्रतिच्छेद करता है. तब BD की लम्बाई $\sqrt{a}$ होगी.

चित्र - 9: $\sqrt{a}$ का निरूपण

यह आसानी से सत्यापित किया जा सकता है कि $\triangle ABD$ और $\triangle DBC$ समरूप है. अतः समरूपता गुणधर्म के अनुसार
\[\frac{AB}{BD} = \frac{BD}{BC} \Rightarrow BD = \sqrt{AB.BC} = \sqrt{a}.\]

किसी धनात्मक रचनीय संख्या $a$ के लिए $\sqrt{a}$रचनीय संख्या होती है.

अभी तक हमने केवल रचनीय संख्याओं के उदाहरण दिए हैं. क्या आप किसी ऐसी संख्या का उदाहरण दे सकते हैं जो रचनीय नहीं है? एक ऐसी ही संख्या $\sqrt[3]{2}$ है. लेकिन यह प्रमाणित करना आसान नहीं है कि यह संख्या अरचनीय है. इस पर और अन्य अरचनीय संख्याओं पर चर्चा हम अगले अनुच्छेदों में करेंगे. परन्तु उससे पहले हम कार्तीय समतल में क्रमित युग्मों की रचनीयता पर चर्चा करेंगे.

कार्तीय समतल में बिंदुओं का निरूपण

चित्र - 10: कार्तीय समतल में बिंदुओं का निरूपण

आप ज्यामिति की कक्षाओं में कार्तीय समतल और इसपर बिंदुओं के निरूपण से अवश्य परिचित हुए होंगे. मान लीजिए $\alpha$ और $\beta$ रचनीय संख्याएँ हैं. तब कार्तीय समतल में बिंदुओं $(\alpha, 0)$, $(0, \beta)$ और $(\alpha, \beta)$ का निरूपण आसानी से किया जा सकता है.इस समतल में  $x$-अक्ष और रेखा $x = \alpha$ का प्रतिच्छेद बिंदु $(\alpha, 0)$ है. इसी प्रकार $y$ -अक्ष और रेखा $y = \beta$ का प्रतिच्छेद बिंदु $(0, \beta)$ है तथा रेखाओं $x = \alpha$ व $x = \beta$ का प्रतिच्छेद बिंदु $(\alpha, beta)$ है. विलोमतः यदि कार्तीय समतल में $(\alpha, \beta)$ रचनीय हों, तो इस बिंदु से $x$-अक्ष और $y$-अक्ष पर लम्ब खींचकर बिंदुओं $A = (\alpha, 0)$ और $B = (0, \beta)$ का निरूपण किया जा सकता है. तब $OA = \alpha$ और $OB = \beta$ होगा. इस प्रकार $(\alpha, \beta)$ की रचनीयता से $\alpha$ और $\beta$ की रचनीयता भी सत्यापित होती है. 

यदि $\alpha$ और $\beta$ रचनीय संख्याएँ हों, तो

• कार्तीय समतल में  बिंदुओं  $(\alpha, 0)$, $(0, \beta)$ और $(\alpha, \beta)$ की रचना की जा सकती है.
• कार्तीय समतल में रेखाओं $x = \alpha$ और $y = \beta$ की रचना की जा सकती है.

विलोमतः, यदि कार्तीय समतल में  बिंदु $(\alpha, \beta)$ रचनीय हों, तो संख्याएँ $\alpha$ और $\beta$ रचनीय संख्याएँ होती हैं.

त्रिकोणमितीय संख्याओं की रचनीयता

चित्र - 11: $\cos\alpha$ और $\sin\alpha$ का निरूपण

प्रारंभिक ज्यामिति की कक्षा में आप पैमाना और परकार की सहायता से कोणों की रचना से अवश्य परिचित हुए होंगे. आपने सीखा होगा कि 15 डिग्री के गुणज के किसी भी कोण की रचना की सकती है. साथ ही आपने कोणों को समद्विभाजित करना और कोण के बराबर कोण की रचना करना भी सीखा होगा. इन प्रक्रियाओं के द्वारा कुछ वैसे कोणों की भी रचना की जा सकती है, जो 15 के गुणज नहीं हैं. इन कोणों को हम रचनीय कोण (constructible angles) कहेंगे. ध्यान दें कि कोणों की रचना में केवल पैमाना और परकार के प्रयोग की अनुमति है. त्रिकोणमिति की कक्षा से आप त्रिकोणमितीय अनुपातों (trigonometrical ratios) से भी परिचित होंगे. यहाँ पर हम इस विषय पर विस्तृत चर्चा नहीं करेंगे. हम यह मानकर चलेंगे कि आपको ये सारी बातें ज्ञात हैं. 

चित्र - 12: $\tan\alpha$ का निरूपण

मान लीजिए $\alpha$ एक रचनीय कोण है. तब $\cos \alpha$, $\sin \alpha$ और $\tan \alpha$ और इनका कोई भी संयोजन रचनीय होता है. विलोमतः, यदि $\cos \alpha$ रचनीय हों, तो $\sin \alpha$, $\tan \alpha$ और साथ ही कोण $\alpha$ रचनीय होता है. इसे चित्र - 11 और चित्र - 12 की सहायता से समझा जा सकता है.

सर्वप्रथम मान लीजिए कि एक रचनीय कोण $\alpha$ दिया गया है. अर्थात हम एक ऐसे कोण की रचना कर सकते हैं, जिसका मान $\alpha$ है. तब हम ऐसे रेखाखंडों की रचना करना चाहते हैं, जिनकी लम्बईयाँ $\cos \alpha$, $\sin\alpha$ और $\tan \alpha$ हैं. इसके लिए कार्तीय समतल में मूल बिंदु O को केंद्र मानकर इकाई त्रिज्या वाला एक वृत्त खींचिए. अब मूल बिंदु O पर $\angle AOB = \alpha$ की रचना कीजिए, जहाँ बिंदु $A$ $x$-अक्ष पर स्थित है और बिंदु B इस कोण की भुजा OB और वृत्त का प्रतिच्छेद बिंदु है (चित्र - 11 देखिए). तब बिंदु B क्रमित युग्म $(\cos \alpha, \sin \alpha)$ को निरूपित करता है. अब बिंदु B से $x$-अक्ष और $y$-अक्ष पर क्रमशः लम्ब BA और BC खींचिए जो इन अक्षों को क्रमशः A और C पर प्रतिच्छेद करते हैं. तब $OA = \cos \alpha$ और $OC = \sin \alpha$ है. विलोमतः, यदि $\cos\alpha$ रचनीय हों, तो $x$-अक्ष पर इसी लम्बाई का एक रेखाखंड OA खींच सकते हैं. क्योंकि $\sin \alpha = \sqrt{1 - cos^2\alpha}$, अतः $\sin\alpha$ भी रचनीय है और $y$-अक्ष पर हम इस लम्बाई का एक रेखाखंड OC खींच सकते हैं. इस प्रकार हम दो रेखाएँ $x = cos\alpha$ और $y = \sin \alpha$ भी खींच सकते हैं, जो क्रमशः बिंदुओं A और C से गुजरते हैं और बिंदु  B पर प्रतिच्छेद करते हैं. अब रेखाखंड OB की रचना कीजिए. तब $\angle AOB = \alpha$ होगा. इसी प्रकार हम दिखा सकते हैं कि एक कोण $\alpha$ रचनीय होता है यदि और केवल यदि $\tan\alpha$ एक रचनीय संख्या हों (चित्र - 12 देखिए).

• एक कोण $\alpha$ रचनीय होता है यदि और केवल यदि $\cos \alpha$ रचनीय होता है.
• एक कोण $\alpha$ रचनीय होता है यदि और केवल यदि $\sin \alpha$ रचनीय होता है..
• एक कोण $\alpha$ रचनीय होता है यदि और केवल यदि कार्तीय समतल में  बिंदु $(\cos \alpha, \sin\alpha)$ रचनीय होता है. 

अरचनीय संख्याएँ और ज्यामितीय आकृतियों की रचनाओं की प्राचीन समस्या

केवल पैमाना और परकार की सहायता से कुछ ज्यामितीय आकृतियों की रचना की असंभवता का अरचनीय संख्याओं से व्यापक संबंध है. ये समस्याएँ ज्यामिति की प्राचीन और रोचक समस्याएँ हैं और इन समस्याओं का इतिहास भी अत्यंत रोचक है. इस विषय पर विशद चर्चा यहाँ संभव नहीं है, क्योंकि इसे समझने के लिए, आधुनिक बीजगणित के अंतर्गत रैखिक बीजगणित (linear algebra) और क्षेत्र-सिद्धांत (field theory) का ज्ञान आवश्यक है. जिज्ञासु पाठक इस लेख के अंत में दिए गए संदर्भ पुस्तकों का अध्ययन कर सकते हैं. भविष्य में इस वेबपृष्ठ पर इस विषय पर विस्तृत लेखन किया जाएगा. परन्तु यहाँ हम इस विषय पर संक्षिप्त चर्चा करेंगे और उपरोक्त समस्याओं पर चर्चा करेंगे. परन्तु इससे पहले कुछ आधारभूत संकल्पनाओं से परिचित होना आवश्यक है.

एक बहुपद (polynomial) $p(x) = a_nx^n + a_{n-1}x^{n-1}+ \cdots + a_2x^2 + a_1x+ a_0$ को परिमेय गुणांक (rational coefficients) वाले घात $n$ का बहुपद कहा जाता है, यदि अचर $a_0, a_1, \ldots, a_n$ परिमेय संख्याएँ हों और $a_n$ शून्येतर हों. यदि $n =0$, तो संगत बहुपद $a_0$ को अचर बहुपद कहा जाता है. जिस बहुपद का घात धनात्मक संख्या हों, उसे हम अतुच्छ बहुपद कहेंगे. परिमेय गुणांकों वाले किसी अतुच्छ बहुपद $p(x)$ को परिमेय संख्याओं के समुच्चय $\mathbb{Q}$ पर अखंडनीय बहुपद (irreducible polynomial) कहा जाता है यदि इसे परिमेय गुणांकों वाले दो अतुच्छ बहुपदों के गुणनफल के रूप में नहीं लिखा जा सके. उदाहरण के लिए, $\frac{3}{2}x^3 - 2x + 5$ परिमेय गुणांकों वाला घात $3$ का बहुपद है, परन्तु $\sqrt{3}x^2 + 2x - 1$ परिमेय गुणांकों वाला बहुपद नहीं है, क्योंकि इस बहुपद का एक गुणांक $\sqrt{3}$ परिमेय नहीं है. बहुपद $x^2 + 1$ $\mathbb{Q}$ पर अखंडनीय है, परन्तु बहुपद $x^2 + 2x + 1$ $\mathbb{Q}$ पर अखंडनीय नहीं है, क्योंकि $x^2 + 2x + 1 = (x+1)(x+1)$. किसी दिए गए बहुपद के अखंडनीयता का  निर्णय करना अत्यंत कठिन हो सकता है. इसके लिए कई सिद्धांत है, जिसपर विस्तृत चर्चा किसी अन्य लेख में की जाएगी. एक वास्तविक संख्या $\alpha$ को किसी बहुपद $p(x)$ का शून्यक (zero or root) कहा जाता है, यदि यह समीकरण $p(x) = 0$ को संतुष्ट करता हों. किसी वास्तविक संख्या $\alpha$ को वास्तविक बीजीय संख्या (real algebraic number) कहा जाता है यदि यह संख्या परिमेय गुणांकों वाले किसी अतुच्छ बहुपद का शून्यक हों. उदाहरण के लिए, $\sqrt[3]{2}$ एक बीजीय संख्या है, क्योंकि यह बहुपद $x^3 - 2$ का शून्यक है. अब हम इस स्थिति में आ गए हैं कि किसी संख्या के अरचनीय होने के प्रतिबंधों पर चर्चा कर सके.

कोई रचनीय संख्या $\alpha $ आवश्यक रूप से  बीजीय संख्या होता है. इस प्रकार यदि कोई वास्तविक संख्या $\alpha$ बीजीय नहीं हों, तो वह संख्या  रचनीय संख्या नहीं हो सकती.

उदाहरण के लिए, $\pi$ रचनीय संख्या नहीं है, क्योंकि यह बीजीय संख्या नहीं है. इस तथ्य की उपपत्ति अत्यंत कठिन है और इसकी उपपत्ति सबसे पहले लिंडेमान (Lindemann) ने 1882 में दी थी. इस प्रकार केवल पैमाना और परकार की सहायता से $\pi$ को संख्या रेखा पर दर्शाना असंभव है. एक दूसरा उदाहरण है - संख्या $e$. यह भी बीजीय संख्या नहीं है और इसलिए यह भी रचनीय संख्या नहीं है. इस तथ्य की उपपत्ति सर्वप्रथम हरमाइट (Hermite) ने  1873 में दी थी. इस विषय पर अत्यधिक जानकारी के लिए संदर्भ [2], [3] और [4] देखें.

एक स्वाभाविक प्रश्न उठता है कि रचनीय संख्याओं की संख्या अधिक है या अरचनीय संख्याओं की ? यह जानकर आपको आश्चर्य होगा कि अरचनीय संख्याएँ रचनीय संख्याओं की अपेक्षा अधिक हैं और "अधिक" से तात्पर्य है कि अरचनीय संख्याएँ अगणनीय (uncountable) हैं जबकि रचनीय संख्याएँ गणनीय (countable) हैं. गणनीयता का अर्थ है कि रचनीय संख्याओं और प्राकृत संख्याओं में एकैक संगति (one-one correspondence) है. इसकी विस्तृत व्याख्या हम गणनीयता से संबंधित किसी लेख में करेंगे.

अब हम किसी संख्या के अरचनीय होने का एक और प्रतिबंध देते हैं.

यदि कोई वास्तविक संख्या $\alpha$ परिमेय गुणांकों वाले किसी ऐसे अतुच्छ और $\mathbb{Q}$ पर अखंडनीय बहुपद का शून्यक हों, जिसका घात $n$ हों और  $n \neq 2^k$, जहाँ $k \geq 1$, तो वह संख्या  रचनीय संख्या नहीं हो सकती.

उदाहरण के लिए, वास्तविक संख्या $\sqrt[3]{2}$ रचनीय संख्या नहीं है, क्योंकि यह बहुपद $x^3 - 2$ का शून्यक है, परन्तु यह बहुपद है अखंडनीय है और इसका घात 2 का घात नहीं है. इस प्रकार केवल पैमाना और परकार की सहायता से $\sqrt[3]{2}$ को संख्या रेखा पर निरूपित नहीं किया जा सकता है.

ज्यामितीय आकृतियों की अरचनीयता

इस अनुच्छेद में हम कुछ ज्यामितीय आकृतियों की रचना से संबंधित कुछ प्राचीन समस्याओं पर चर्चा करेंगे. ध्यान रहें कि ज्यामितीय रचना से हमारा तात्पर्य है - केवल पैमाना और परकार की सहायता से रचना.

वृत्त के क्षेत्रफल के बराबर क्षेत्रफल वाले वर्ग की रचना की समस्या

किसी दिए गए वृत्त के क्षेत्रफल के बराबर क्षेत्रफल वाले वर्ग की रचना करना संभव नहीं है. मान लीजिए कि दिए गए वृत्त की त्रिज्या 1 है. अतः इसका क्षेत्रफल $\pi$ होगा. हम एक ऐसे वर्ग की रचना करना चाहते हैं जिसका क्षेत्रफल $\pi$ हों. यदि यह रचना संभव हों, तो मान लीजिए कि इस वर्ग की भुजा $a$ है. तब इसका क्षेत्रफल $a^2$ होगा, जो $\pi$ के बराबर होना चाहिए. अर्थात $a^2 = \pi$. क्योंकि $a$ रचनीय संख्या है, अतः $a^2$ भी रचनीय संख्या होगी और इसीलिए $\pi$ भी रचनीय संख्या होगी. क्योंकि कोई भी रचनीय संख्या आवश्यक रूप से बीजीय संख्या होती है, अतः $\pi$ एक बीजीय संख्या होनी चाहिए. परन्तु, हम पहले ही चर्चा कर चुके हैं कि $\pi$ बीजीय संख्या नहीं है. अतः हमारा यह मानना गलत है कि वर्ग की भुजा $a$ एक रचनीय संख्या है. अतः भुजा $a$ की रचना पैमाना और परकार की सहायता से नहीं की जा सकती है. इस प्रकार $\pi$ क्षेत्रफल वाले वर्ग की रचना संभव नहीं है.

किसी घन के आयतन के दुगुने आयतन वाले घन की रचना की समस्या

किसी दिए गए घन के आयतन के दुगुने आयतन वाले घन की रचना करना संभव नहीं है. मान लीजिये कि दिए गए घन की भुजा $1$ है, तब इसका आयतन भी $1$ होगा. हम एक ऐसे घन की रचना करना चाहते हैं जिसका आयतन $2$ हों. यदि यह संभव हों, तो हम घन की एक भुजा $a$ की रचना कर सकते हैं जिससे कि इसका आयतन $a^3 = 2$ होगा. तब $a = \sqrt[3]{2}$ एक रचनीय संख्या होगी, क्योंकि हमने माना था कि भुजा $a$ रचनीय है. परन्तु हम पहले ही चर्चा कर चुके हैं कि $\sqrt[3]{2}$ रचनीय संख्या नहीं है. अतः इस भुजा की रचना संभव नहीं है और इस प्रकार उपरोक्त घन की भी रचना संभव नहीं है.

किसी कोण को समत्रिभाजित करने की समस्या

आपने ज्यामिति की कक्षा में कोणों को समद्विभाजित करना अवश्य सीखा होगा. प्रांत यह सदैव संभव नहीं है कि किसी कोण को समत्रिभाजित किया जा सके. अर्थात कुछ ऐसे कोण हैं जिन्हें तीन बराबर भागों में विभाजित करना संभव नहीं है. उदाहरण के लिए, $60^{\circ}$ का कोण लीजिए. इस कोण को पैमाना और परकार की सहायता से समत्रिभाजित करना असंभव है. यदि ऐसा संभव होता, तो हम $20^{\circ}$ के कोण की रचना करने में सक्षम होंगे. परन्तु तब $\cos 20^{\circ}$ की रचना संभव होगी. इस प्रकार $\cos 20^{\circ}$ एक रचनीय संख्या होगी. मान लीजिए $a = 2 \cos 20^{\circ}$. तब $a$ एक रचनीय संख्या होगी. त्रिकोणमितीय सूत्र से हम जानते हैं कि $\cos 60^{\circ} = \frac{1}{2}$
\[\cos 60^{\circ} = 4\cos^3 20^{\circ}- 3\cos 20^{\circ} \Rightarrow \frac{1}{2} = 4\cos^3 20^{\circ}- 3\cos 20^{\circ}.\]
इसलिए
\[1 = 8\cos^3 20^{\circ}- 3(2\cos 20^{\circ}) \Rightarrow (2\cos20^{\circ})^3- 3(2\cos 20^{\circ}) - 1 = 0. \]
अर्थात $a^3 - 3a - 1 = 0$. इस प्रकार संख्या $a$ परिमेय गुणांकों वाले एक अखंडनीय बहुपद $x^3 - 3x - 1 $ का शून्यक है. क्योंकि इस बहुत का घात $2$ के घात के बराबर नहीं है. अतः अरचनीयता की दुसरे प्रतिबंध के अनुसार यह संख्या रचनीय संख्या नहीं है. अतः हम $\cos 20^{\circ} = \frac{a}{2}$ भी रचनीय संख्या नहीं है. परन्तु तब कोण $20^{\circ}$ भी रचनीय कोण नहीं होगा. अतः $20^{\circ}$ के कोण को समत्रिभाजित करना असंभव है.

समबहुभुज की रचना की समस्या

पैमाना और परकार की सहायता से समबाहु त्रिभुज, वर्ग, समपंचभुज और समषट्भुज की रचना करना आसान है. परन्तु इससे अधिक भुजाओं वाले समबहुभुज की रचना संभव नहीं भी हो सकती है. उदाहरण के लिए, समसप्तभुज की रचना असंभव है. यदि यह संभव होता तो हम $(\frac{360}{7})^{\circ}$ के कोण की रचना कर पाएँगे. अतः $a = 2\cos(\frac{360}{7})^{\circ}$ एक रचनीय संख्या होनी चाहिए. त्रिकोणमितीय सूत्रों की सहयता से यह दिखाया जा सकता है कि यह संख्या परिमेय गुणांकों वाले बहुपद $x^3 + x^2 -2x - 1$ का शून्यक है. यह बहुपद $\mathbb{Q}$ पर अखंडनीय है, परन्तु इसका घात $2$ के किसी घात के बराबर नहीं है. इसलिए, अरचनीय संख्याओं के द्वितीय प्रतिबंध के अनुसार $a$ रचनीय संख्या नहीं है. अतः हमारा यह मानना गलत था कि $(\frac{360}{7})^{\circ}$ के कोण की रचना की जा सकती है. अतः समसप्त्भुज की रचना संभव नहीं है. व्यापक रूप में, निम्नलिखित कथन सत्य है:

$n$-भुजाओं वाले समबहुभुज की (तुल्यतः कोण  $(\frac{360}{n})^{\circ}$ की) रचना  संभव होता है यदि और केवल यदि $\phi(n)$ दो का कोई घात होता है. यहाँ  $\phi(n)$ ऑयलर फाई फलन है, जो $n$ या इससे कम ऐसे संख्याओं  $a$ की संख्या बताता है जिससे कि $\gcd(a, n) = 1$.

इस कथन की उपपत्ति यहाँ देना संभव नहीं है, क्योंकि इसके लिए क्षेत्र - सिद्धांत की व्यापक जानकारी आवश्यक है.

संदर्भ पुस्तकें व शोध पत्र

[1] P. B. Bhattacharya, S. K. Jain and S. R. Nagpaul, Basic Abstract Algebra, 2nd Ed., Cambridge University Press, 1995.

[2] I. N. Herstein, Topics in Algebra, 2nd Ed., John Wiley $\&$ Sons, 1975.

[3] G. H. Hardy and E. M. Wright, An Introduction to the Theory of Numbers first published 1938, fifth Edition 1979 with additions 2000, Clarendon Press, Oxford U.K.

[4] Underwood Dudley, A Budget of Trisections, Springer- Verlag: New York, 1987.

[5] I. Niven, A simple proof that π is irrational. Bull. Amer. Math. Soc. 53, (1947). 509.



प्रथम दो पुस्तकें [1] और [2] अमूर्त बीजगणित की पुस्तक हैं और इसमें  क्षेत्र - सिद्धांत पर विस्तृत अध्ययन - सामग्री उपलब्ध है. पुस्तक [1] में पृष्ठ संख्या 358 - 364 पर रचनीयता पर विस्तृत सामग्री उपलब्ध है. पाठक पुस्तक [2] में पृष्ठ संख्या 228 - 231 पर भी इस विषय पर सामग्री उपलब्ध है. इसी पुस्तक में पृष्ठ संख्या 216 - 219 पर वास्तविक संख्या $e$ के अबीजीयता की भी उपपत्ति प्रस्तुत की गई है. पुस्तक [3] संख्या - सिद्धांत की पुस्तक है. इस पुस्तक में पृष्ठ संख्या 170 - 176 पर $e$ और $\pi$ की अबीजीयता की उपपत्तियाँ दी गई हैं. शोध पत्र [5] में $\pi$ के अपरिमेयता की एक सरल उपपत्ति दी गई है. पुस्तक [4] कोणों के समत्रिभाजन समस्या पर एक रोचक पुस्तक है. इसमें उन सभी व्यक्तियों का परिचय दिया गया है, जिन्होंने कोणों के समत्रिभाजन का असफल प्रयास किया. साथ ही उनकी ज्यामितीय रचनाओं को भी प्रस्तुत किया गया है. इस  पुस्तक में पैमाने और परकार के अतिरिक्त अन्य उपकरणों की सहायता से किसी कोण के समत्रिभाजन पर भी चर्चा की गई है.